Fraude électorale américaine: Benford peut-il dénoncer une manipulation au profit de Biden ?

Par Claude Timmerman

Ancient élève Ecole Normale Supérieure de ST Cloud (aujourd’hui Lyon) prom. 69. Biologiste : zoologie, paléontologie, génétique et génétique des populations ; démographie. Statisticien : modélisations et statistiques biologiques et critique des méthodologies médicales. Spécialiste des questions environnementale et de l’analyse de l’Évolution. Analyste de la surpopulation et des effets de la densification humaine croissante sur le milieu, notamment de son impact sur les espèces aujourd’hui en voie de disparition. Militant de la première heure dans la lutte contre les OGM, les pesticides, la chimie agricole et les saccages environnementaux liés aux nouvelles pratiques agricoles mal gérées (Remembrements, irrigation, etc.) Ancien conseiller pour les questions agricoles et environnementales du gouvernement togolais de la présidence Eyadéma. Ancien chargé de mission du Ministre du Développement Rural togolais. Il signe régulièrement des articles sur Boulevard Voltaire,Medias-presse-info et le blog Terre-future. Il est aussi Conférencier et rédacteur au CEP (Centre d’Etude et de Prospective). Catholique traditionaliste, ancien cérémoniaire pontifical du cardinal Veuillot, notamment lors d’un pèlerinage en Terre Sainte (1965) où il a découvert l’importance des églises primitives et séparées et les rapports islamo-chrétiens pluricentenaires associés notamment au statu quo à Jérusalem. Il s’est beaucoup intéressé au monde coranique et à la civilisation islamo-perse d’Asie Centrale. Aujourd’hui en retraite, résolument opposé aux thèses du concile Vatican II et au mythe nouveau du « judéo-christianisme » qui en a découlé,  qu’il considère comme un oxymore. Il a publié à ce sujet un ouvrage : Judéo-christianisme – Travestissement historique et Contre-sens idéologique.

A l’époque où le monde médiatique, qui a unilatéralement annoncé la victoire du candidat démocrate sans aucune confirmation officielle, révèle son adhésion active et globale à une manipulation électorale – dont Joe Biden s’est lui-même vanté dans une vidéo qu’il n’a jamais contestée, et qui a fait le tour du monde malgré la censure diligentée par toutes les instances dirigeantes des réseaux sociaux et des sites d’hébergement de vidéos – certains, sûrement pleins de bonne volonté, tentent de montrer que cette fraude peut être mise en évidence par un instrument statistique comme ce fut le cas en Suisse après l’introduction du vote électronique, dès 2012.

https://www.letemps.ch/sciences/statisticiens-traquent-fraude-electorale

Et les militants antifraude de brandir alors la loi de Benford dont la fonction de répartition (image de la distribution) peut effectivement notoirement s’écarter pour Biden de son profil classique, présentant des anomalies en cas de fraude : c’est ce qui exploité aujourd’hui aussi en matière de cyber criminalité et pour détecter la fraude fiscale. Ce dont maintenant certains médias se font l’écho.

C’est là qu’il importe que le lecteur soit familiarisé avec cette loi peu connue, sinon il risquerait de gober n’importe quoi – comme il y est déjà contraint de le faire par ces mêmes médias qui diffuse la propagande officielle alarmiste « anti-covid » établie par des gens qui ne savent pas de quoi ils parlent, et des médicâtres qui la relayent..

La loi de Benford

A la différence de lois de probabilité les plus anciennes connues où – à partir d’un modèle mathématique construit – on a mis évidence des phénomènes qui les suivent, la loi de Benford est une loi de probabilité empirique initialement fondée sur l’observation de phénomènes réels et non intuitifs, mais à partir desquels on a trouvé un modèle mathématique approchant. D’où son surnom de « loi des nombres anormaux ».

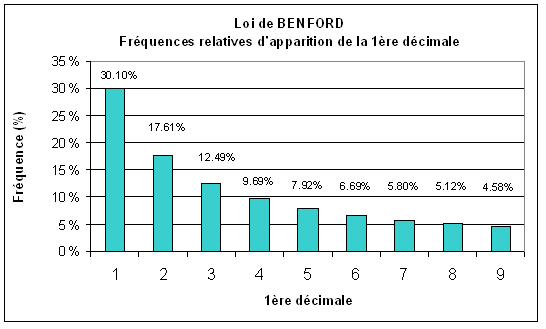
Ainsi, dans une série de données numériques décimales, on pourrait ainsi s’attendre à voir les chiffres de 1 à 9 apparaître après la virgule à peu près aussi fréquemment comme premier chiffre significatif, soit avec une fréquence de 1/9 = 11,1 % pour chacun d’eux : c’est une conséquence « attendue » de la construction d’un système établi sur une numération en base 10. Or cette approche intuitive s’avère fausse !
Historiquement, en 1881, c’est l’astronome Simon Newcomb, qui l’énonce dans le Journal of Mathematics, après s’être aperçu de l’usure (et donc de l’utilisation préférentielle) des premières pages des tables de logarithmes et que, par suite, les nombres décimaux à première décimale « 1 » ont une fréquence d’apparition et d’usage significativement plus importante que les autres.

Personne ne s’intéressera à cette remarque jusqu’à ce que Frank Benford, en 1938, remarque à son tour cette usure inégale, et arrive aux mêmes résultats que Newcomb, après avoir répertorié des dizaines de milliers de données de sujets des plus divers (longueurs de fleuves, cours de la bourse, etc.)
C’est à partir de ces observations empiriques que la loi de probabilité fut formalisée : elle porte, à tort ou à raison le nom de Benford (quand la paternité pourrait en être attribuée à Newcomb même s’il n l’a pas réellement formalisée).

C’est initialement une loi dite discrète (discontinue, construite point par point) qui sera généralisée en loi continue.

Définition :
Une série de nombre réels en écriture décimale suit la loi de Benford si la fréquence d’apparition du premier chiffre significatif c vaut approximativement :

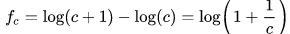
Pour 1 ≤ c ≤ 9 où log désignant le logarithme décimal. ¹

L’une des probabilités très intéressante à analyser qui découle de cette formalisation initiale est celle du second chiffre et celle du troisième, si le premier chiffre de la série concernée suit effectivement la loi de Bandford.

La probabilité que le chiffre c [c ϵ (1 ;… ; 9] soit en position k > 1 est donnée par la relation :

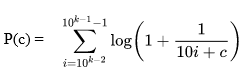
Une formule qui se démontre assez facilement et qui peut paraître un peu rébarbative mais qui est assez facilement manipulable par les outils de calcul, même élémentaires.

Disposer des probabilités (traitées alors au seuil de signification souhaité) des chiffres de la succession décimale de valeurs dont les chiffres initiaux sont susceptibles de suivre la loi de Benford permet de mettre en évidence des « anomalies » observées par rapport aux séries attendues.
Ce sont les anomalies ainsi détectables qui peuvent être l’indice de manipulations de données.
Évidemment, il existe des tas de séries statistiques qui ne peuvent suivre une telle loi : par exemple l’analyse de la répartition des tailles chez l’homme ne risque pas de faire apparaître « 1 » en première décimale dans la série (même si on s’intéresse plus spécifiquement aux pygmées). C’est ce qu’on appelle un biais statistique structurel.

Les applications sont multiples dans les domaines littéraires, scientifiques, économiques et financiers.

Plusieurs démonstrations mathématiques indépendantes ont pourtant confirmé que ce résultat non intuitif est tout à fait attendu dans de nombreux contextes.
Ainsi, en multipliant deux à deux n’importe quels nombres aléatoires, on aboutit à une série de valeurs qui vérifie peu ou prou la «loi de Benford». Voir par exemple ici :

https://docs.google.com/spreadsheets/d/1pnk6fsVJRcYH4dksD2XpVBOxSVoAfCX83rZJ_QRTuXE/edit#gid=0

Comme le résumaient en 2008 les chercheurs Gauvrit et Delahaye, «la loi de Benford [est] naturelle si les nombreux facteurs qui expliquent telle ou telle grandeur agissent multiplicativement».
Autrement dit, dans de nombreuses situations «en vie réelle» où les valeurs étudiées sont le fruit d’interactions parfois complexes, il n’y a finalement rien d’étonnant à observer une répartition plus ou moins similaire à celle définie par la «loi» de Benford dans les domaines les plus variés (tels ici les effectifs de cheptels !).

https://calque.pagesperso-orange.fr/langages/python/pybenford.html

A contrario toute série de valeurs dont la succession observée des chiffres des nombres donnés s’éloigne notablement de la distribution de Benford peut être susceptible de suspicion de données frauduleuses, sans que la fraude à ce stade soit en aucun cas avérée.
Il est même possible de mesurer le « doute probabiliste » associé en chaque point entre la valeur observée et la valeur théorique supposée fc de Benford : la distance correspondante peut être calculée par exemple avec le test classique de χ2 et traitée ensuite en terme de seuil acceptable et de compatibilité… ou non.
Ces données font alors l’objet d’analyses de services de recherche spécialisés dans des domaines aussi variés que la fraude fiscale, les falsifications de données financières et boursières, etc.
Selon une étude de 2011, la Grèce était « le pays de la zone euro dont les comptes publics s’écartaient le plus de la répartition attendue par la loi de Benford. » (sic !)

L’analyse cryptographique où les mots les plus fréquemment employés sont recensés et listés par nombre décroissant permet de déterminer une « caractéristique rédactionnelle » de l’auteur d’un texte qui sera possiblement distinct du signataire officiel…

En biométrie, les applications sont multiples notamment pour rechercher des résultats fantaisistes dont certaines publications – surtout médicales et pharmaceutiques – sont truffées.
En revanche la détection d’anomalies ainsi observées peut aussi être précieuse en termes de recherche pure.
Ainsi l’analyse simultanée de gènes ou portions de gènes d’intérêt via le séquençage à haut débit (NGS) montre un décompte qui suit (sauf anomalie pathologique ainsi détectable dans le lot traité) une loi de Benford :

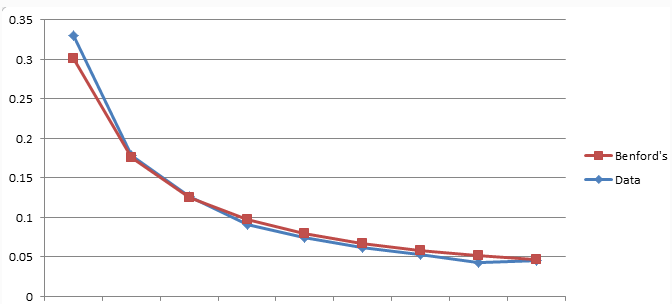
https://www.louvainmedical.be/fr/article/le-next-generation-sequencing-ou-ngs-un-nouvel-outil-de-biologie-moleculaire-au-service-des

Le problème de la fraude électorale

C’est en Suisse que la loi de Benford a été utilisée pour la première fois dans cette perspective.
«Jusqu’à 25% des votants utilisent le système électronique», relève Michel Warynski, directeur du support et des opérations de vote à la Chancellerie d’État. Il rappelle toutefois que, quel que soit le canal de vote, il n’est pas possible de totalement exclure une manipulation.
Le recours à la loi de Benford a été mis en œuvre lors des élections du 25 novembre 2012 dans le canton de Genève
Pour Eva Cantoni, professeure au Research Center for Statistics et au Département de sciences économiques de l’Université de Genève, «L’utilisation de la loi de Benford dans un tel contexte ne fait pas l’unanimité. La méthode manque en outre de puissance statistique, c’est-à-dire qu’elle permettrait probablement de détecter uniquement une fraude massive.»

https://www.letemps.ch/sciences/statisticiens-traquent-fraude-electorale

La situation quelque peu litigieuse de l’actuelle élection américaine fait précisément état – selon la fameuse déclaration vidéo occulté de Biden – d’une « fraude massive » (sic !)
C’est un certain Jim Hoft qui a jeté le pavé dans la marre de Twitter.

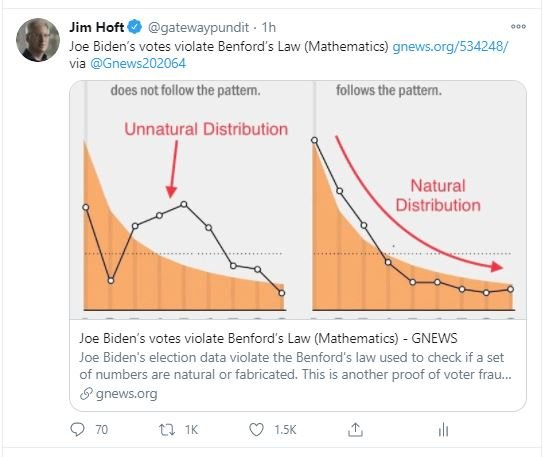
Les graphiques reproduits par monsieur Holt ne donnent ni abscisses ni ordonnées ni chiffres.
S’ils sont pédagogiques en termes d’alerte, ils sont inexploitables tels quels en termes de démonstration!
C’est pourquoi le site gnews.org a repris les graphiques de monsieur Hoft et propose un intéressant ensemble de résultats électoraux de plusieurs grandes villes américaines dans une page au titre fracassant :
“Joe Biden’s votes violate Benford’s Law – (Mathematics)”
(Les votes Biden violent la loi de Benford)

https://gnews.org/534248/

Le schéma global, comparatif cumulé des voix, proposé n’a pourtant rien de particulièrement choquant, sur le plan statistique, au regard de cette loi, bien au contraire !

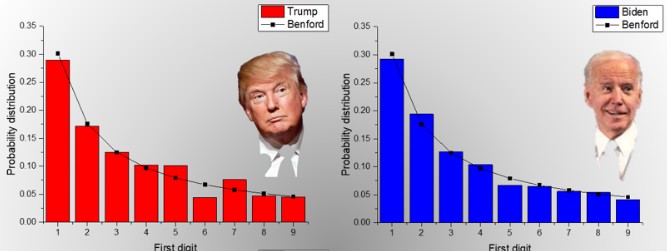
C’est en fait l’analyse bureau par bureau de votes dans certaines agglomérations qui va poser problème et notamment les cas du comté de Milwaukee – Wisconsin

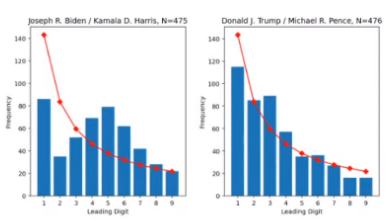
de Chicago – Illinois

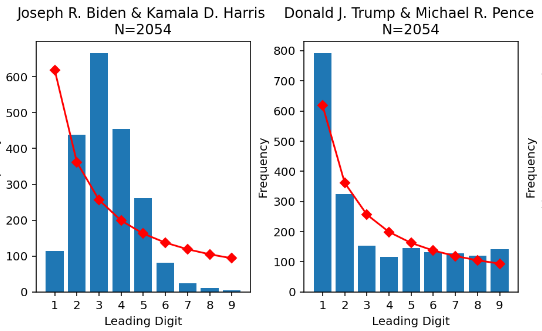
Ou du comté d’Alleghany (Pittsburg) – Pennsylvanie

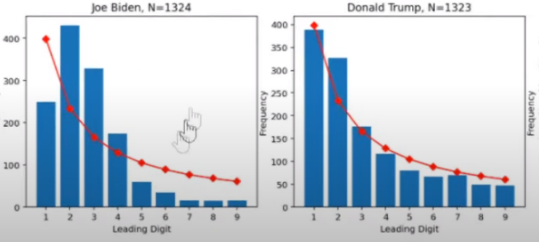
Ou d’autres où les profils de Joe Biden sont carrément « hors des clous » alors qu’ils sont conformes dans de nombreux autres cas également présentés.

Le cas de Milwaukee a immédiatement fait réagir les universitaires
Daniel Vidali Fryer, professeur de statistique à l’Université de Queensland, constate que la proportion du nombre de votants dans les 347 bureaux de vote la ville de Milwaukee n’épouse pas le profil de la «loi de Benford» et s’en écarte fortement, mais il explique immédiatement que cela «n’a absolument rien d’anormal».
Il apporte la  » justification » suivante :
«Il faut commencer par examiner la répartition des votants dans les circonscriptions électorales de Milwaukee. Ce nombre est, majoritairement, compris entre 500 et 1 000 votants par bureau. Regardons maintenant la répartition de la proportion des voix reçues par Biden dans chaque bureau : elles sont presque toujours supérieures à 50 %, avec une moyenne à 73 %. Or, 73 % d’un nombre compris entre 500 et 1 000 est un nombre compris entre 365 et 730. Rien dans la fourchette 365-730 n’a pour premier chiffre significatif « 1 ». Il est donc parfaitement attendu, dans ce contexte, que 1 ne soit pas le chiffre le plus courant.»
«On pourra objecter que ces calculs se basent sur le taux de 73 %, qui est justement jugé suspect par certains. Ce n’est en réalité pas un problème, car nous ne chercherons pas à calculer la proportion « réelle » d’électeurs favorables à Biden. Nous ne faisons que répondre à la question : « Si l’ensemble des données est fiable, alors donne-t-il lieu à une distribution de Benford ? » Car, logiquement, cette question équivaut à « si la distribution n’est pas de Benford, alors cela signifie-t-il qu’elle n’est pas fiable ? » Tout cela se résume donc à la question de savoir si une élection valide et digne de confiance pourrait donner lieu aux proportions que nous observons. Le seul cas où nous pourrions nous attendre à cela est celui où un candidat est hautement préféré – et à Milwaukee, nous nous attendons déjà à ce que Biden soit hautement préféré.»

Le lecteur aura donc avalé donc cela sans broncher ?
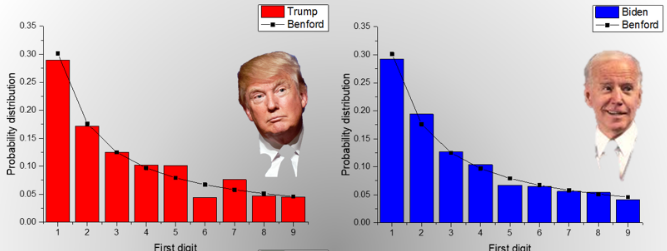
N’importe qui pourtant pourrait rétorquer que si dans certains endroits « on peut s’attendre » à un résultat de 75% pour Biden qui « explique les écarts par rapports à la loi de Benford », on peut tout autant s’attendre à voir des écarts équivalents pour Trump dans des zones où il est plébiscité et  » hautement préféré »…
Curieusement les propagandistes de Biden, si actifs dans les médias, sont bien incapables de montrer de telles courbes impliquant Trump !

Daniel Vidali Fryer, comme d’autres mathématiciens, a réalisé diverses simulations électorales qui tiennent compte de la taille des bureaux et des intentions de vote, et confirment que les écarts à la loi de Benford sont tout à fait attendus. Alors pourquoi cela ne concerne-t-il pas Trump ?
Les malversations électorales sont un sujet pourtant très étudié aux USA :

https://projecteuclid.org/download/pdfview_1/euclid.ss/1330437932

«Les tests statistiques ne donnent jamais une preuve de fraude, mais indiquent seulement si les résultats semblent inhabituels», rappelait aussi Eva Cantoni, de l’Université de Genève, dans un entretien au quotidien Le Temps en 2013.
Elle estimait que, dans le contexte d’élections à Genève, «par le jeu du hasard, environ un scrutin sur dix semblera inhabituel par rapport à la loi de Benford, même si aucun problème n’a entaché le processus».

La loi de Benford ne peut donc pas être invoquée systématiquement pour démontrer à coup sûr l’existence d’une fraude. Au mieux cela peut être un indice, au pire une fausse piste.
Il n’empêche qu’il y a des indices à suivre !
Il faut donc s’en remettre aux techniques parfois laborieuses qui ont fait leurs preuves : la mise en évidence des bourrages d’urnes, des votes multiples attribués à une même personne ou aux morts.
D’une manière générale, quand le nombre de votes enregistré dans un bureau est supérieur au nombre d’inscrits on peut sans trop s’avancer conclure à l’existence d’une fraude…
Et dans le cas des dernières élections américaines, ces pratiques semblent avoir été très largement utilisées.
Faut-il vouloir le prouver
Claude Timmerman

¹ Pour ceux qui souhaiteraient disposer d’éléments mathématiques plus conséquents sur l’axiomatique associée, nous les renvoyons aux articles suivants qui donnent une assez bonne approche les concernant

• le calcul des limites, associé à la fonction ⱬ de Riemann :
  https://www.maths-france.fr/MathSpe/GrandsClassiquesDeConcours/SeriesDeFonctions/FonctionZetaDeRiemann.pdf
• la loi de Bandford : https://fr.wikipedia.org/wiki/Loi_de_Benford
• la convergence avec la loi de Zipf : https://fr.wikipedia.org/wiki/Loi_de_Zipf